Developing a Simple Programming Language - Part 5: Parenthesized Expressions

Are you excited as much as I am? Today is the day we’ll complete our calculator, and start getting into the good stuff. We’ll be adding parenthesized expressions to our grammar, and implementing an interpreter that will be able to evaluate parenthesized expressions. We’ll be able to evaluate expressions like 6 + 2 * (10 - 3 / (12 / 4) + 1).

First of all, let’s update our grammar to support expressions inside parenthesis.

Take a look at our grammar from the last chapter. Our factor production is used for basic units in expressions. Today, we’ll be adding another basic unit - a parenthesized expression. So, this is what our updated grammar will look like.

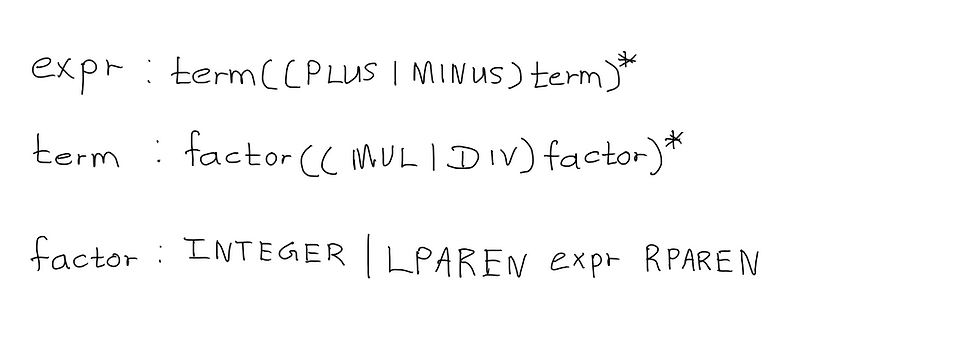
In our factor rule, we have introduced two new terminals; LPAREN for left parenthesis “(“, and RPAREN for right parenthesis “)”. Additionally, the non-terminal expr is between LPAREN and RPAREN. The syntax diagram for factor is as follows:

Think about how we are going to write this in our Parser. You might have noticed something interesting this time, which is the fact that our factor() method is now recursive. If we try to interpret something like 12 / (3 + 1), we will start off with the expr() method, and eventually get to a point where we will recursively use expr() again to compute the (3 + 1) part of the arithmetic expression.

We will be making the following changes to our code:

LPAREN, and RPAREN tokens will be added to the Type enum.

enum Type {
   INTEGER,
   PLUS,
   MINUS,
   MUL,
   DIV,
   LPAREN,
   RPAREN,
   EOF
}

Update the getNextToken() method in our Lexer to catch LPAREN and RPAREN tokens.

private Token getNextToken() {
   while (this.currentChar != Character.MIN_VALUE) {
       if (Character.isWhitespace(this.currentChar)) {
           skipWhitespace();
           continue;
       }
       if (Character.isDigit(this.currentChar)) {
           return new Token(Type.INTEGER, integer());
       }
       if (this.currentChar == '+') {
           advance();
           return new Token(Type.PLUS, currentChar);
       }
       if (this.currentChar == '-') {
           advance();
           return new Token(Type.MINUS, currentChar);
       }
       if (this.currentChar == '*') {
           advance();
           return new Token(Type.MUL, currentChar);
       }
       if (this.currentChar == '/') {
           advance();
           return new Token(Type.DIV, currentChar);
       }
       if (this.currentChar == '(') {
           advance();
           return new Token(Type.LPAREN, currentChar);
       }
       if (this.currentChar == ')') {
           advance();
           return new Token(Type.RPAREN, currentChar);
       }

       try {
           throw new Exception("Invalid token type");
       } catch (Exception e) {
           System.err.printf("Invalid token type %c found", currentChar);
           System.exit(0);
           return null;
       }
   }
   return new Token(Type.EOF, null);
}

Update factor() in our Parser

/*
factor : INTEGER | LPAREN expr RPAREN
 */
int factor() {
    Token token = lexer.getCurrentToken();
    if (token.getType() == Type.INTEGER) {
        lexer.eat(Type.INTEGER);
        return (int) token.getValue();
    } else {
        lexer.eat(Type.LPAREN);
        int result = expr();
        lexer.eat(Type.RPAREN);
        return result;
    }
}

Let’s try compiling, and running our interpreter.

$ javac -d . Token.java
$ javac -d . Lexer.java
$ javac -d . Parser.java
$ javac -d . Main.java
$ java Main

calc> 8 - 2 * (12 / (12 / (2 + 2) - 1))
-4
calc> 8 - 2 * (12 / (12 / (2 + 2) - 1)) / (1 + 3) + 8 + 2 - (10)
5
calc> 2 + (((5 + 3)))
10                                    

Congratulations on making it all the way to the end! You have learned how to create an interpreter that can evaluate complex arithmetic expressions. We have completed our calculator interpreter (sort of).

In the next chapter, we will talk about an important, and widely used data structure used in compiler and interpreter design. We will be using this data structure throughout this tutorial series.

Previous Chapter: Part 4: Associativity, Precedence, and Grammars

Next Chapter: I'm working on it. Be patient :)